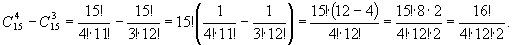1) id_004 ответы конкурсного тура
2) Руководитель команды Мишустина Татьяна Николаевна
3) К поиску ответов приступили 20.11.2006
4) Ответы готовы 30.11.2006
5) Технический исполнитель Мишустина Татьяна Николаевна
6) URL веб-странички с ответами конкурсного тура http://Dvazdy-dva-2.narod.ru
7) Таблица ответов

№ задания	Решение задачи и ответ
1	Для решения составим таблицу: Ваня Петя Саша Коля Не С Не В В Не П Не В Не С - Не В П К - C Из 1) известно, что Ваня не С. Из 2) Петя не В, не С, А Ваня не В. Коля ниже П, а П ниже П, значит Коля не П, и не В. Таким образом Саша носит фамилию на букву В. Значит Колина фамилия начинается на С. Т.К. Саша и Петя одного роста, то Петя не может носить фамилию на П., значит его фамилия начинается на К. А Ване досталась фамилия на П.
2	Чтобы имена и отчества составляли династию, то одинаковых имен должно быть четное количество для промежуточных членов династии: отца деда и прадеда. А значит мистером Х или его прапрадедом может быть только Иван Семенович или Василий Васильевич. Но ни у кого не имени Василий, кроме самого Василия Васильевича, значит он прапрадед. Сопоставляя имена и отчества имеем династическую цепочку: Иван Семенович – Семен Иванович – Иван Иванович – Иван Васильевич – Василий Васильевич. Поэтому прадеда мистера Х зовут Иван Васильевич.
3	Количество списков определяет число перестановок без повторений, а именно 10!
4	Для того, чтобы узнать сколько человек изучало французский и немецкий языки нужно из общего количества 20 человек вычесть тех, кто изучал по одному языку и по два оставшихся, т.е. немецкий и английский и французский и английский: 20-(3+6+1+3)=5. 5 человек изучало французский и немецкий языки.
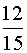5	Неблагоприятное для нас событие будет, если два подарка будут не мишки. Вероятность этого события. Вероятность вынуть первого не мишку , а второго не мишку, при условии, что первого вынули не мишку 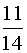. Значит вероятность того, что две вынутые игрушки будут не мишки – 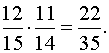Чтобы найти вероятность того, что из двух подарков будет хотя бы один мишка нужно из 1 вычесть вероятность неблагоприятного события Вероятность того, что Маше достанется хотя бы один мишка –
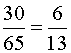6	Всего конфет 65. Значит вероятность вынуть «Мишку на Севере» – , «Ананасную» – 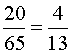, «Красную Шапочку» –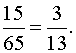
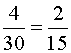7	Вероятность вынуть выигрышный билет , невыигрышный 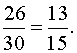Вероятность того, что из четырех вынутых билетов 2 выигрышных
8	Из одной буквы можно составить 3 слова, из 2-х 9 слов, из трех – 27 слов, из четырех 81. Значит всего можно составить 120 слов.
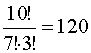9	Так как в комиссию входит один математик, значит остальные семь – экономисты. Из 10 экономистов можно составить комиссию из 7 человек способами. Так как по условию математиков должно быть хотя бы 1, то их может быть и больше. Если математиков 2, то экономистов 6, и их можно скомплектовать 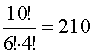способами, если математиков 3, то экономистов 5, их можно скомплектовать 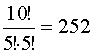способами, если экономистов 4, то 210 способа, если их 3, то 120 способами, если экономистов 2, то 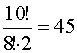способов, если экономистов 1, то 10 вариантов. Подсчитаем общую сумму: 120+210+252+210+120+45+10=967. Экономистов можно укомплектовать 967 различными способами. Т.к. про математиков ничего не сказано, то комплектацию по математикам подсчитать нельзя.
10	5 номеров: 12хххх, х12ххх, хх12хх, ххх12х, хххх12.
-	Дополнительные задания
1	Экипаж можно составить 11 способами.
2	Данная задача не имеет однозначного решения. Можно только указать пределы, в которых находятся количество «вундеркиндов». Допустим, что в олимпиаде по английскому языку участвовали только участники олимпиады по математике. Тогда, для того, чтобы хотя бы в одной олимпиаде участвовали все ученики класса, необходимо, чтобы в олимпиаде по информатике обязательно участвовали ученики, не принимавшие участия ни в одной олимпиаде. Схематически такая ситуация выглядит так: 30 человек – количество учеников класса ; 23 человека – участники олимпиады по математике ; 19 человек – участники олимп.по англ. языку ; 16 человек – участники олимп. по информ. ; Таким образом, в классе есть 5 человек, которые участвовали во всех олимпиадах. Другая «крайняя» ситуация. На олимпиаду по английскому языку пошли все ученики, которые не участвовали в олимпиаде по математике. А на олимпиаду по информатике обязательно пошли ученики, которые уже участвовали в двух олимпиадах. Схематически такая ситуация выглядит так: 30 человек – количество учеников класса ; 23 – «математики» 19 – «англичане»- ; 16 - «информатики» ; В этом случае, число учеников, принявших участие в трех олимпиадах – наибольшее, а именно 12 человек.. Таким образом , в классе может быть от 5 до 12 «вундеркиндов».
3	Количество списков определяет число перестановок без повторений, а именно 10!
4	1)Количество анаграмм для слова точка равно количеству перестановок букв в этом слове, т.е 5!= 120 слов. 2)Количество анаграмм для слова «абракадабра» равно количеству перестановок с повторениями, т.к. некоторые буквы встречаются не один раз– «а» - 5, «б» - 2, «р» -2. 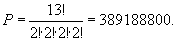3)Аналогичным образом определяем количество анаграмм для слова «комбинаторика». В этом слове не один раз встречаются буквы: «к» - 2, «о» - 2, «и» - 2, «а» -2.
5